光学谐振腔(optical resonant cavity)是光波在其中来回反射从而提供光能反馈的空腔。它是激光器的必要组成部分,通常由两块与激活介质轴线垂直的平面或凹球面反射镜构成。
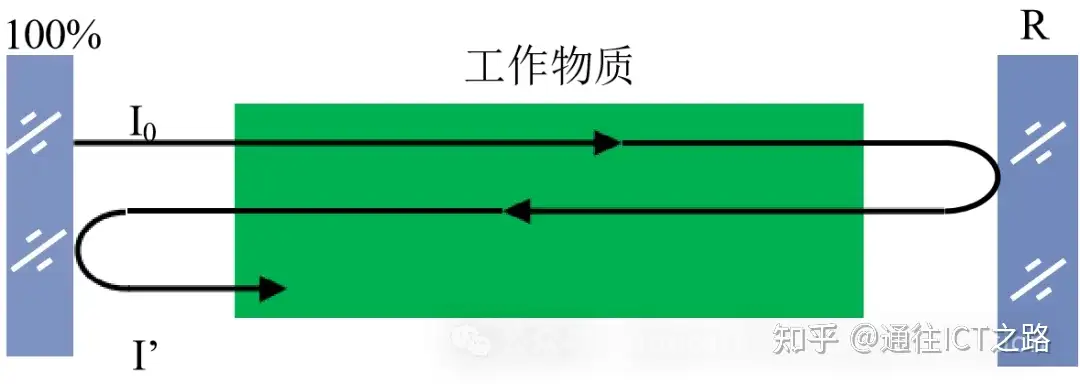
图1:在激活物质的两端恰当地放置两个反射镜片(球面镜或平 面镜),就构成一个最简单的光学谐振腔。
光学谐振腔的模式,也称为腔内的电磁场分布,能够在经历一个完整的往返后自我复制。具体来说,这意味着电磁场的幅度分布(包括光的相位)在往返一次后必须保持一致,除了可能发生的光功率损失。
这些模式在几何结构稳定的谐振腔中存在,而在不稳定的谐振腔中,其模式特性则较为复杂。在激光谐振腔、法布里-珀罗干涉仪和模式清洁器(图2)等应用中,这些模式扮演着至关重要的角色。

图2:模式清洁器,由两个透镜和一个针孔组成。
在最基本的情况下,仅由抛物面镜和均匀介质构成的谐振器,其模式遵循Hermite-Gaussian模式。其中,最基本的模式是高斯模式,其场分布由高斯函数描述(即高斯光束)。光束半径和波前的曲率半径的变化取决于谐振器的具体设计。
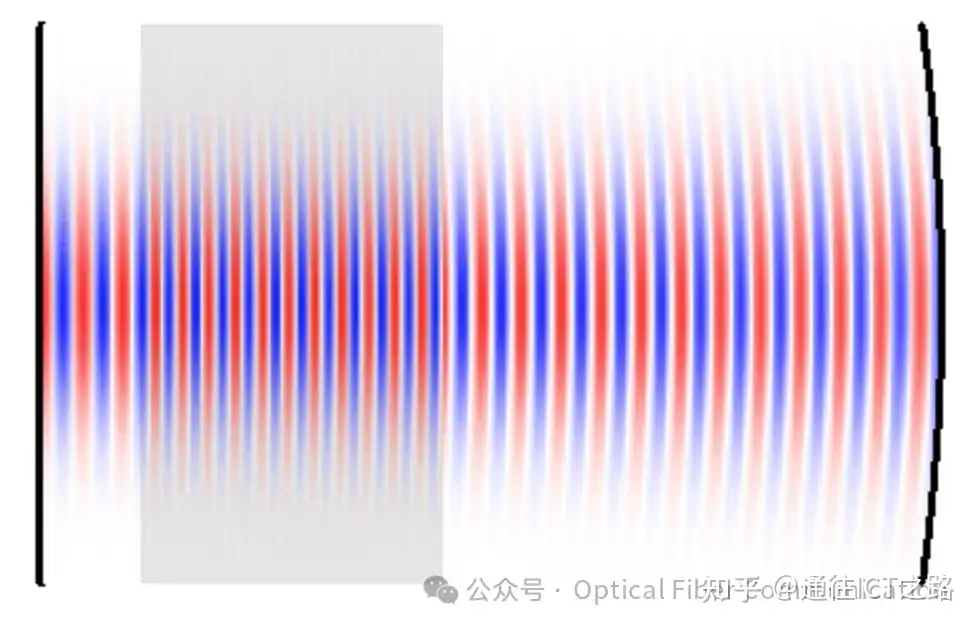
图3:展示简单谐振器及其高斯模式的电场分布。波前在平坦的左端镜上必须是平面的,并且左镜上的光束半径要与右镜的曲率相匹配。
例如,上图3和图4展示了由平面镜、激光晶体和弯曲端镜组成的两种不同配置的简单谐振器的高斯模式。在端镜曲率更大的情况下(如图4),左镜上的模式半径会减小。可以看到,从左侧开始的具有平坦波前的光束(适合平面镜)在传播到右侧时会扩展,以匹配另一镜子的形状,实现包括波前形状在内的场配置的自我复制。此外,往返的相位差应为2π的整数倍。
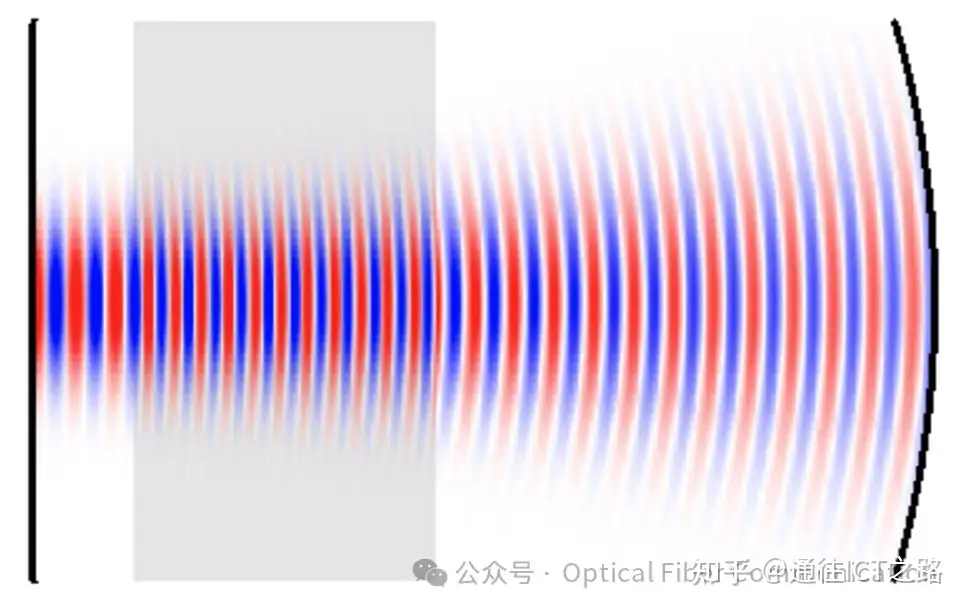
图4:与图3相同,但右侧镜子的曲率更大。
如果右端镜向相反方向弯曲(即凸面),则不存在高斯模式,此时我们面对的是一个不稳定的谐振器。这种谐振器虽然也有模式,但其形状更为复杂。大多数激光器在稳定状态下工作,且存在高斯模式的谐振器中。
对于上述简单谐振器,可以通过相对简单的方程来计算模式参数。然而,对于更复杂的谐振器配置,如涉及多个曲面镜和其他光学元件(例如具有热透镜效应的激光晶体),通常需要数值软件来计算模式属性。
除了高斯模式,稳定的谐振器还具有强度分布更复杂的高阶模式。在光束的腰部,电场分布可以表示为两个阶数为n和m(非负整数,分别对应于x和y方向)的高斯函数的乘积。(我们仍然假设一个简单的谐振器,仅包含抛物面镜和光学均匀介质。这些模式也称为TEMnm模式。这种模式的光强度分布(如图3)在水平方向有n个节点,在垂直方向有m个节点(如图5)。
如果已知基模的高斯光束半径,则可以很容易地计算出所有高阶模式的模式分布。

图5:TEMnm模式的强度分布。
对于光学共振,振幅分布不仅必须在一次往返后保持其形状,而且还要经历2π的整数倍的相位变化。这仅适用于特定的光学频率。因此,这些模式由三个指数来表征:横向模式指数n和m,以及轴向模式数q(往返相位变化除以2π)。
在某些重要情况下,我们会使用TEM_{nmq}这样的标记来包含轴向模式编号。当n等于0且m等于0时,这些模式被称作轴向模式(或称为基模、高斯模式),而其他所有模式则被称作高阶模式或高阶横向模式。
请注意,由于Gouy相移,光学频率不仅取决于轴向模式数,还取决于横向模式指数n和m(见图6)。
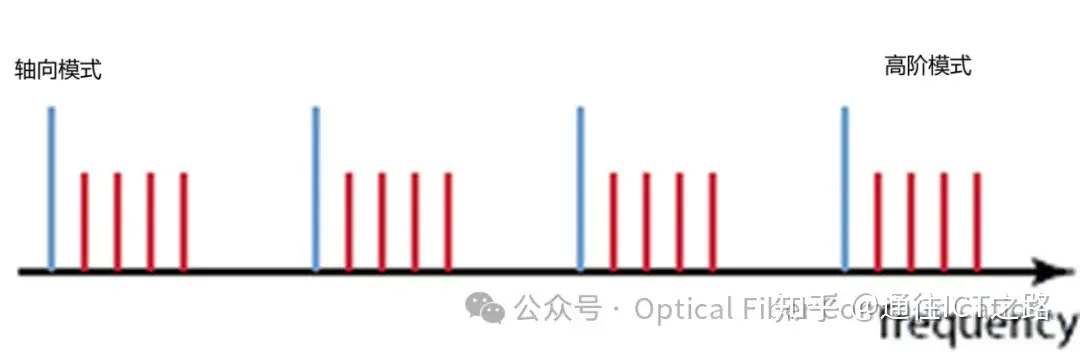
图6:光谐振器的模式频率。
忽略色散的情况下,我们有:
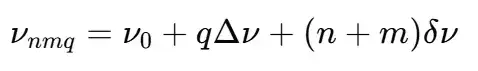
其中Δν是自由光谱范围(轴向模式间距),δν是横向模式间距。后者可以计算为:
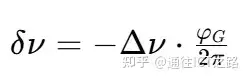
其中φG是每次往返的Gouy相移。Gouy相位的大小取决于谐振器的设计。
由于色散和衍射效应,模式间隔实际上具有(弱的)频率依赖性,但这通常并不重要。
在光学频率范围内,可以进行共振增强,例如,入射光波从外部撞击谐振器的部分透射镜。该范围的宽度称为谐振器带宽,这个量由光功率损耗率决定。
对于Gouy相移的某些值,可能会出现模式频率简并。在激光器中,这些简并会通过轴向模式与高阶模式的共振耦合导致光束质量的严重恶化。通过适当的谐振器设计,至少可以避免特别敏感的频率简并,从而提高激光束质量。这种简并也可能具有有用的特性;例如,当法布里-珀罗干涉仪用作光谱分析仪时,反射镜的精确调整(例如在共聚焦配置中)允许在没有模式匹配的情况下使用。此外,简并腔可用于Herriot型多通道单元,例如,在不改变整体谐振腔设计的情况下,用于大幅增加激光谐振器中的往返路径长度。
连续波操作中的激光振荡通常发生在一个或多个频率上,这些频率与某些模式频率相当精确。然而,与频率相关的增益会导致一些频率牵引(略微非谐振振荡),并且模式频率本身可能会受到增益介质中的热透镜效应等的影响。
激光器的单频操作意味着只有一个谐振器模式(几乎总是高斯模式)被激发;这导致发射带宽比激发多个谐振器模式的情况低得多。
如果在连续波操作中同时激发激光谐振器的不同模式,则通常会出现模式竞争现象。
当激光器的光束质量较差时,这通常(尽管并非总是)是高阶横腔模式激发的结果。当输出光被发送到快速光电二极管时,可以检测到涉及高阶模式的节拍音符,即频率大大偏离往返频率的整数倍。
在锁模操作中,光谱是一个频率梳,由完全等距的光谱线组成(忽略可能的激光噪声),其中线间距是反向脉冲重复率。由于模式频率不完全等距,因此发射频率和模式频率之间存在一定程度的不匹配;失配越大,锁模器件(例如可饱和吸收器)的效果就越强。基于这一见解,很容易理解为什么在色散较大的情况下,很难在宽发射带宽和相应较短的脉冲持续时间下实现模式锁定。
无源谐振器的模式具有一定的频率带宽,这是由于功率损耗对腔内磁场的阻尼。如果一个谐振器往返后的光功率是原始功率的ρ倍(即每次往返的小数损耗为1 – ρ),往返时间为T_rt,则谐振带宽为:

激光谐振器的模式可能与空谐振器的模式有很大不同,因为它们会受到横向变化的增益和损耗的影响。这不仅会导致空间形状的一些变形;也是因为谐振器模式不再是相互正交的。
相反,有一组伴随模式,通过一些双正交关系与实际的谐振器模式相关。这种双正交(非正态)性质具有许多奇特的含义。例如,激光器中循环的总功率不再只是在不同模式下传播的功率之和。
经Optical fiber communication授权发布
